8.15 Test for difference between proportions
If two samples are drawn from different populations, we may be interested in finding out whether the difference between the proportion of successes is significant or not. Let x1 and x2 be the number of items possessing the attribute A, in the random sampling of sizes n1 and n2 from two populations respectively.
Then the sample proportions of successes are 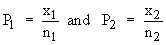 if P1 and P2 are proportion of successes in the two populations and Q1 = 1 - P1, Q2 = 1 - P2 then if P1 and P2 are proportion of successes in the two populations and Q1 = 1 - P1, Q2 = 1 - P2 then
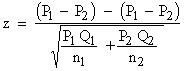
Under the hypothesis that the proportions in two populations are equal.
i.e. P1 = P2 = P Þ Q1 = Q2 = Q (say) then
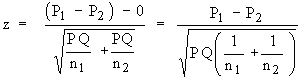
In general, however, we do not know the populationís proportion of success. In such a case we can replace P by its best estimate P = the pooled estimate of the actual proportion in the population, where
Pooled estimate (P) = 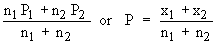
Example A machine produced 20 defective
articles in a batch of 500. After overhauling it produced 3 defective
in a batch of 100. Has the machine improved ?
Solution: Ho : P1
= P2 i.e. The machine has not improved after overhauling
Ha : P1 Ļ P2
Now P1 = 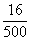 = 0.032 and P2 = = 0.032 and P2 = 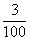 = 0.030 = 0.030
Pooled estimate of actual proportion in the population is given by
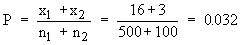
Q = 1 - P = 0.968
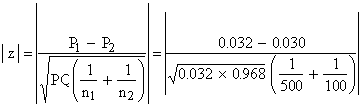
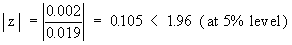
Ho is true i.e. the machine has not improved significantly.
|