|
Example In a sample of 900 stock-holders
of companies, 400 stated that their major aim in holding stocks
is capital appreciation. What is the 90% confidence range within
which lies the population proportion of stock-holders who hold stocks
for capital appreciation ?
Solution: The 90% confidence range is given by P' ± 1.64
S.E. where S.E. = 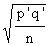
Now P' = 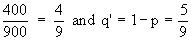
Hence the range is given by 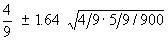
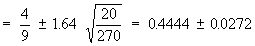
Hence the range is 0.4444 + 0.0272 = 0.4716 and
0.4444 - 0.0272 = 1.4172
ie. ( 0.4172 to 0.4716 ).
* Note that when we do not know po and qo then we can use p' and q' in their places respectively.
Example Out of consignment of 10000 tennis balls, 400 were
selected randomly and examined. it was found that 20 of these were
defective. How many defective balls you can reasonably expect to
have in the whole consignment at 95% confidence level ?
Solution: P' = 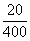 = 0.05 and q' = 1 - p = 0.95 = 0.05 and q' = 1 - p = 0.95
The limits are ( at 95% confidence level ) = p' ± 1.96 S.E.
where S. E. = 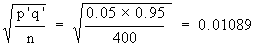
Therefore, 0.05 ± 1.96 ´ 0.01089 i.e. 0.05 ± 0.0213
Therefore p' lies between 0.0713 to 0.0287.
The expected number lies between
NP' = 10000 ´ 0.0713 = 7130 and
NP' = 10000 ´ 0.0287 = 2870.
|