|
Example Past records show that the mean
marks of students taking statistics are 60 with standard deviation
of 15 marks. A new method of teaching is adopted and a random sample
of 64 students is chosen. After using the new method, the sample
gives the mean marks of 65. Is the new method better?
Solution: Here we are interested in knowing
whether the marks increased on using the new teaching method. Therefore,
we use the one-tailed method:
The null hypothesis is : Ho : m
= 60
The alternative hypothesis is : Ha :
m > 60.
We have 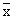 = 65, m = 60, s = 16 and n = 64 then
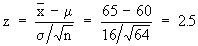
Now suppose the researcher had predetermined the
level of significance which is 0.01 or 1% for his decision. Then
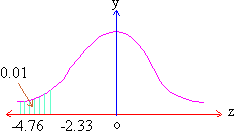
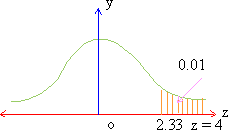
2.5 > 2.33 (Here z-score is 2.33 for 0.01 level on the upper-tail
of distribution). Therefore, the observed value is highly significant.
That is Ho is rejected and Ha is accepted.
This means the new teaching method is better.
Example A manufacturer of an antibiotic
claimed that his antibiotic was 90% effective in curing a certain
type of V. D. if used for a duration of 8 weeks. In a sample of
200 people who tried this, 160 people were cured. Determine whether
his claim is legitimate.
Solution: Let P = Probability for curing
the V. D. by the use of the manufacturer’s antibiotic.
Setting two types of hypothesis as :
Null hypothesis :Ho : P = 0.9 Þ claim is supported.
Researcher's hypothesis : Ha : P <
0.9 Þ claim is rejected.
Now P' = Proportion of success in the given sample =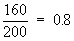 
Now P = 0.9 Þ q = 0.1
Therefore,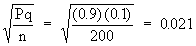
Thus the corresponding z-score will be
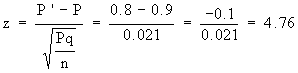
which is much less than - 2.33. Thus by our decision
rule Ho is rejected and Ha is accepted stating
that his claim is not legitimate and that the sample results are
highly significant (at 0.01 level of significance ).
Example The breaking strengths of metal
rods, produced by a certain company, have mean as 820 kg. and standard
deviation as 50 kg. When a new manufacturing process is adopted,
it is claimed that the breaking strength can be improved. A sample
of 100 rods is tested and the results indicates that the breaking
strength as 840 kg. Can we support this claim at a 1% level of significance
?
Solution: Setting up the two hypotheses
as :
Null hypothesis :Ho : m = 820 kg. Þ there is no change.
Researcher's hypothesis : Ha : m < 820 kg. Þ Breaking strength is improved.
A one-tailed test should be used at 0.01 level of significance for decision making rule.
Now m = 820,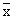
= 840, n = 100 and s = 50 then
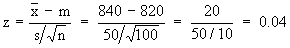
Now z-score 4 > 2.33 i.e. the null hypothesis Ho is rejected and the researchers hypothesis is accepted stating that we support the claim "Breaking strength is improved by the new manufacturing process".
Note: In practice, one should adopt a
'one tailed test' only when he has enough reasoning to expect that
the difference will be in a specified direction. A two-tailed test
is conservative than a one-tailed test. Since it uses more extreme
test statistic for the rejection of the null hypothesis.
|
