|
Thus there is no reason
to reject Ho. To find the limits,
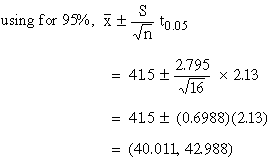
Example Ten individuals are chosen at
random from the population and their heights are found to be inches
63, 63, 64, 65, 66, 69, 69, 70, 70, 71. Discuss the suggestion that
the mean height in the universe is 65 inches given that for 9 degree
of freedom the value of studentís 't' at 0.05 level of significance
is 2.262.
Solution: xi = 63, 63, 64,
65, 66, 69, 69, 70, 70, 71 and
n = 10
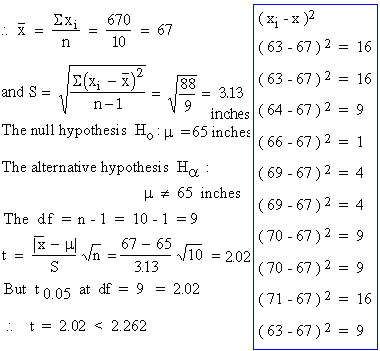
The difference is not significant
at a t 0.05 level thus Ho
is accepted and we conclude that the mean height is
65 inches.
Example Nine items of a sample have
the following values 45, 47, 50, 52, 8, 47, 49, 53, 51, 50. Does
the mean of the 9 items differ significantly from the assumed population
mean of 47.5 ?
Given that for degree of freedom = 8. P = 0.945 for t = 1.8 and P = 0.953 for
t = 1.9.
Solution: Given that for degree of freedom
= 8. P = 0.945 for t = 1.8 and P = 0.953 for t = 1.9.
\
S xi = 45 + 47 + 52 + 48 + 47 + 49 + 53 + 51 + 50 = 442
n = 9
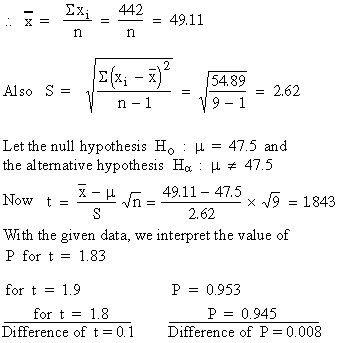
Therefore for difference of t = 0.043,
the difference of P = 0.0034. Hence for t = 1.843, P = 0.9484. Therefore
the probability of getting a value of t
> 1.43 is ( 1 - 0.9484 ) = 0.051 which is in fact 2 ī
0.051 = 0.102 and it is greater than 0.05. Thus Ho is
accepted, i.e. the mean of 9 items differ significantly from the
assumed population mean.
Example A certain stimulus administered to each of 12 patients
resulted in the following increments in 'Blood pressure' 5, 2, 8,
-1, 3, 0, 6, -2, 1, 5, 0, 4. Can it be concluded that the stimulus
will in general be accompanied by an increase in blood pressure,
given that for all df the value of t0.05 = 2.201?
Solution: 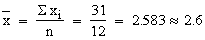
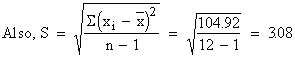
The null
hypothesis Ho : m
= 0 i.e. assuming that the stimulus will not be accompanied by an
increase in blood pressure (or the mean increase in blood pressure
for the population is zero).
Now 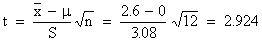
The table
value, t0.05,
n = 11 = 2.201
Therefore, 2.924 > 2.201
Thus the null hypothesis Ho is rejected
i.e. we find that our assumption is wrong and we say that as a result
of the stimulus the blood pressure will increase.
|