|
Example The following table is published
in a memoir written by 'Karl Pearson'
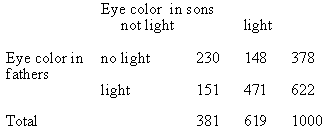
Test whether the color of son’s eyes is associated
with that of father’s.
Solution: The null hypothesis : The eye
color of sons and eye color of father’s are independent. If this
is true the expected frequencies are
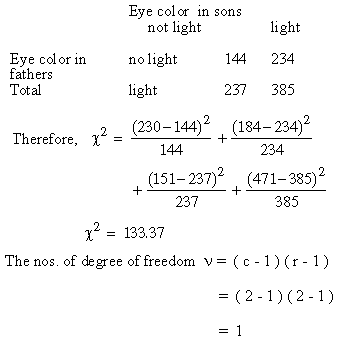
The table
value of c2
at 0.05 level of significance for df = 1 is 3.841 which is extremely
poor compared to the calculated 133.37. Thus we reject the null
hypothesis saying that there is high association between the sons’s
eyes and that of the father.
Example In an experiment on the immunization of goats
from anthrax, the following results were obtained. Derive the you
inference on the efficacy of the vaccine.
| |
|
|
|
| |
Died of anthrax |
Survived | Total |
| |
| |
|
| Inoculated | 2 | 10 | 12 |
| |
|
|
|
| Non-inoculated | 6 | 6 | 12 |
| |
|
|
|
| Total | 8 | 16 | 24 |
Solution: The null hypothesis : Inoculation
of vaccine and survival are independent attributes. The expected
frequencies would be :
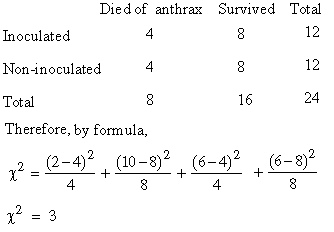
The nos. of degree of freedom n = ( c - 1 ) ( r - 1
)
= ( 2 - 1 ) ( 2 - 1 )
= 1
From the
table c20.05,
n
= 1
= 3.841. Thus the calculated value is less than
table value. Hence the hypothesis is accepted,
Note : Brandt and Snedecor gave a simple
formula for 2 ´
2 contingency table, in order to calculate c2.
Representing th ( 2 ´ 2
) fold contingency table as :
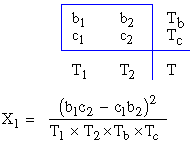
We Multiply diagonal frequencies and find the
difference between the two products ( b1c2
- c1b2
)
Square this i.e. (
b1c2
- c1b2
)2
Multiply by the grand total i.e. (
b1c2
- c1b2
)2
´ T
Divide the above result by the product of all
the sub totals i.e. T1
´T2
´ Tb
´ Tc
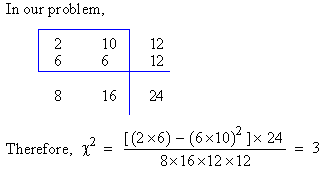
|