|
Use c2
test to assess the correctness of the hypothesis that the digits
were distributed in an equal manner in the tables from which they
are chosen.
Solution: Our hypothesis is that the
digit were distributed equally in the tables as correct. The expected
frequencies of the digits would be :
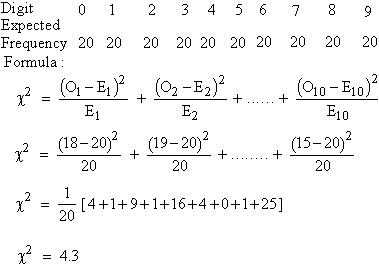
The numbers of degree of freedom r (df)
= ( c - 1 ) ( r - 1 )
=
( 10 - 1 ) ( 2 - 1 )
= 9
From the
table, c20.03,
n = 9 = 16.919
Therefore, 4.3 < 16.919
Thus calculated
value of c2
is less than table value of
c20.05,
n = 9. Hence our hypothesis is correct.
Example In a certain town 100 persons
were randomly chosen and interviewed for their educational stature.
The results are as
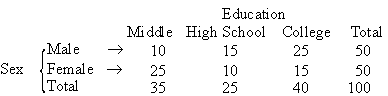
Can you say that education depends on the sex of
the individual?
Solution: The null hypothesis : That
there is no association between education and sex. On this hypothesis
the expected frequencies are as below :
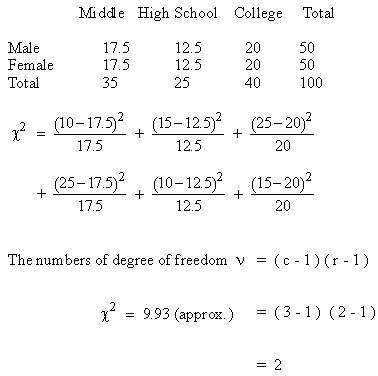
From the
table c20.05,
n
= 2 = 5.99 and c2
0.01,
n
= 2 = 9.21
Thus the
calculated value of c2
is highly significant and the null hypothesis which stated that,
education does not depend on sex is, discredited.
|